Cool Info About What Is The Mean Of T And D

How To Calculate Arithmetic Mean Using Assumed Method Ungrouped
Unlocking the Mystery
Ever stumbled upon the phrase "mean of T and D" and felt a little lost? Don't worry, you're not alone! It might sound a bit cryptic at first, but it's actually a pretty straightforward concept, especially when we break it down. We're going to demystify it, step by step, and by the end of this, you'll be explaining it to your friends!
Think of it like this: "T and D" usually refers to Time and Distance. So, when someone asks for the "mean" of those two things, they're generally looking for some kind of average value related to both. But the tricky part? It's all about context! What are we trying to do with the information? That's what dictates exactly how we calculate the "mean."
For example, imagine you're tracking your commute. "T" is the time it takes you to get to work, and "D" is the distance you travel. The 'mean of T and D' in this case might not be as simple as adding the time and distance and dividing by two. In fact, it probably isn't! Instead, it would depend on what you're trying to figure out (like average speed, perhaps?).
So, let's dive deeper into some common scenarios where you might encounter this intriguing little phrase.
1. Understanding the Context is Key
The biggest mistake people make when trying to figure out the "mean of T and D" is jumping straight to calculations without considering the context. Always, always ask yourself: what problem are we trying to solve? What information are we hoping to extract?
Think of it like baking a cake. You wouldn't just throw all the ingredients together without a recipe, would you? The recipe (or, in this case, the context) tells you how to combine the ingredients to get the desired result. Similarly, the context tells you how to combine "T" and "D" to get the meaningful "mean."
Sometimes, the context is explicit. You might be given a specific formula to use. Other times, you'll have to infer it from the surrounding information. The important thing is to pause and think before reaching for your calculator.
Let's say, for instance, you want to calculate your average speed. You'd use the formula: Speed = Distance / Time. That isn't the arithmetic mean of Distance and Time but is a derived measurement, with Time and Distance as crucial components in the calculation. See? Context is everything!

Alphabet Initials Logo TD, DT, T And D 36769557 Vector Art At Vecteezy
Scenario 1
This is probably the most common scenario where the "mean of T and D" comes into play. Let's say you're driving a car. You travel 100 miles in 2 hours. What's your average speed? Well, you wouldn't add 100 and 2 and divide by 2 (that would give you 51!). Instead, you'd use the formula: Average Speed = Total Distance / Total Time. In this case, 100 miles / 2 hours = 50 miles per hour.
Now, let's make it a little more complex. Suppose you drive 50 miles in the first hour and then 70 miles in the next hour. What's your overall average speed? You need to calculate the total distance (50 + 70 = 120 miles) and the total time (1 + 1 = 2 hours). Then, you divide: 120 miles / 2 hours = 60 miles per hour. See how we're averaging the results and not just the raw "T" and "D" numbers?
But here's a curveball: what if you want to find the average speed, but the times are all the same? Say you drove 60 miles in one hour, then 70 miles in another hour, and then 80 miles in a final hour. Now, finding the arithmetic mean of the distances would actually give you the average speed! (60+70+80)/3 = 70 mph. So, equal time intervals simplify the calculation. Lucky you!
The point is, "mean of T and D" in the context of average speed isn't a single, rigid calculation. It's about applying the correct formula based on the specific information you have.
2. Real-World Speed Examples
Imagine a cyclist training for a race. They might track their distance and time for each training session to monitor their progress. By calculating their average speed for each ride, they can see if they're getting faster over time.
Or, consider a delivery driver. They need to optimize their routes to minimize delivery time. By analyzing their time and distance data, they can identify areas where they're wasting time and find more efficient routes.
Even in logistics, understanding the relationship between Time and Distance is valuable for predicting delivery times and optimizing supply chains.
In summary, think of "mean of T and D" related to speed as meaning you might need to compute Speed as Distance/Time, or Average Speed as (Total Distance)/(Total Time).

Variance And Standard Deviation Formula
Scenario 2
In physics, the "mean of T and D" could refer to something entirely different. Imagine studying the motion of a projectile. "T" might represent the time of flight, and "D" might represent the horizontal distance traveled. A physicist might be interested in calculating the range of the projectile, which depends on both time and distance, but not in a simple average kind of way.
The relationship between time and distance in projectile motion is governed by the laws of physics, including gravity and initial velocity. The formula for range typically involves trigonometric functions and requires a deeper understanding of the underlying principles.
Furthermore, consider the concept of displacement. Displacement is a vector quantity that represents the change in position of an object. It takes into account both the distance and direction of movement. In this context, "D" might represent displacement, and "T" could represent the time interval over which the displacement occurred. The ratio of displacement to time gives us the average velocity.
So, you can see that in physics, the interpretation of "mean of T and D" depends heavily on the specific problem being addressed and the physical laws governing the system.
3. Projectile Examples
A baseball player hitting a home run is classic projectile motion! The time the ball is in the air and the distance it travels are key factors determining if it clears the fence. Physicists (and baseball statisticians!) use these to calculate launch angles and initial velocities.
Think about launching a rocket. Understanding how long it will be in flight and how far it will travel is vital for mission success. Accurately modelling the projectile motion can inform critical design choices.
Even something as simple as throwing a ball to a friend involves projectile motion! We subconsciously adjust our throw to account for the distance and the time it will take for the ball to reach them.

Scenario 3
While less common, the "mean of T and D" could also crop up in statistical analysis. Imagine you're collecting data on the time it takes for a website to load ("T") and the amount of data transferred ("D"). You might want to see if there's a correlation between the two. In this case, calculating a simple arithmetic mean of the time and data would be meaningless. Instead, you'd likely use statistical methods like correlation or regression to analyze the relationship.
Correlation helps you understand the strength and direction of the relationship between two variables. A positive correlation means that as one variable increases, the other tends to increase as well. A negative correlation means that as one variable increases, the other tends to decrease. Regression analysis allows you to build a mathematical model that predicts one variable based on the other.
In our website example, you might find a positive correlation between load time and data transferred — meaning that websites with more data tend to load more slowly. You could then use regression analysis to predict load time based on the amount of data transferred.
However, it's still important to remember that "mean of T and D" isn't really meant to refer to arithmetic mean in this scenario. It's simply a common term for analyzing the overall relationship between time and distance in a statistical context, which requires more sophisticated statistical tools to analyze.
4. Statistical Examples
Analyzing traffic patterns by measuring the time it takes for cars to travel certain distances on the freeway, alongside recording the number of vehicles using the road. This info can help city planners decide on how to adjust traffic control.
Scientists could be tracking how far a certain plant grows from its seeding point over the period of a week or a month. Analyzing the data, scientists can then identify any correlations between plant growth and the time elapsed since seeding, potentially revealing key insights into plant development processes.
A retailer might monitor the amount of time a customer spends browsing and their overall purchase amount to assess how customer engagement influences spending habits.
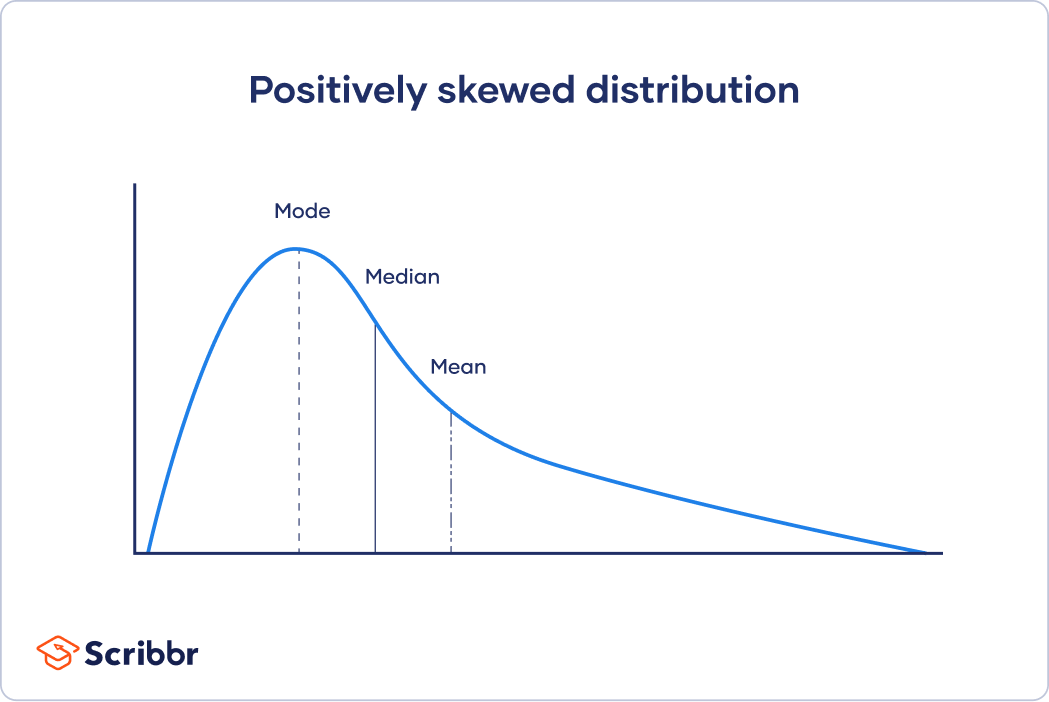
Median Statistics
Key Takeaways and Avoiding Confusion
The "mean of T and D" is not a fixed formula. It's a general term that requires context to understand. Always ask: what are "T" and "D" representing in this specific situation? What problem am I trying to solve?
Often, it involves calculations beyond a simple arithmetic mean. You might need to use formulas from physics, statistics, or other fields. Don't just blindly add and divide!
If you're unsure, clarify the context. Ask the person who used the phrase what they mean by it. A little clarification can save you a lot of time and frustration.
Finally, remember that communication is key. Instead of using the ambiguous "mean of T and D," try to be more specific. For example, instead of saying "Calculate the mean of T and D," say "Calculate the average speed."
5. Common Mistakes to Avoid
Assuming that "mean" always means arithmetic mean. It often doesn't in the context of "T and D."
Ignoring the units of measurement. Make sure your units are consistent before performing any calculations (e.g., convert minutes to hours, or feet to miles).
Forgetting to consider the context. This is the most common mistake of all! Always ask yourself: what problem am I trying to solve?
Failing to communicate clearly. If you're asking someone to calculate something, be specific about what you want them to calculate.
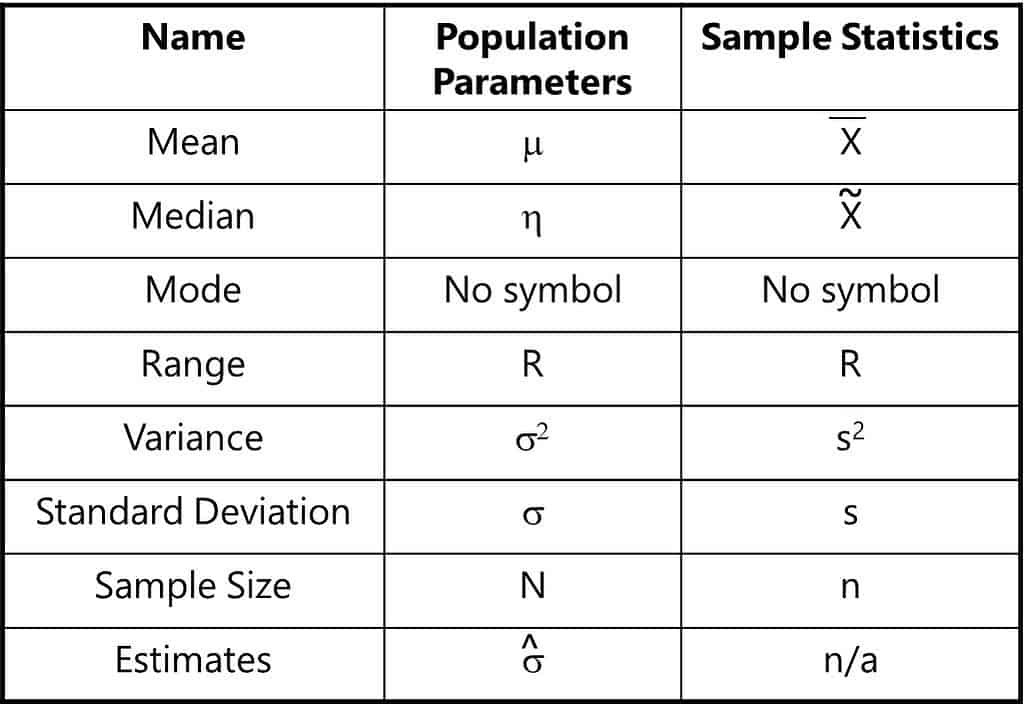
Mean Median Mode Symbols
FAQ
6. Q
A: Most often, "T and D" refers to Time and Distance. However, it's always important to confirm the context!
7. Q
A: Nope! There's no one-size-fits-all formula. The calculation depends entirely on the situation and what you're trying to figure out.
8. Q
A: Rarely. You might use it in very specific statistical analyses, but in most cases, you'll need to use other formulas (like the one for average speed).
9. Q
A: Absolutely! In fact, that's the best approach. Clear communication is always the most efficient way to avoid confusion. Don't be afraid to say, "Could you clarify what you mean by 'mean of T and D' in this case?"