First Class Info About What Is Half Adder And Full

Unveiling the Secrets of Half Adders and Full Adders

Ever wondered how your computer performs complex arithmetic? It all boils down to some pretty neat little circuits called adders. Specifically, we're going to chat about half adders and full adders — the unsung heroes of digital computation. Think of them as the building blocks, the LEGO bricks if you will, that let your device sum things up. They might sound intimidating, but trust me, they're surprisingly straightforward.

1. What's a Half Adder? Think of it as Addition 101

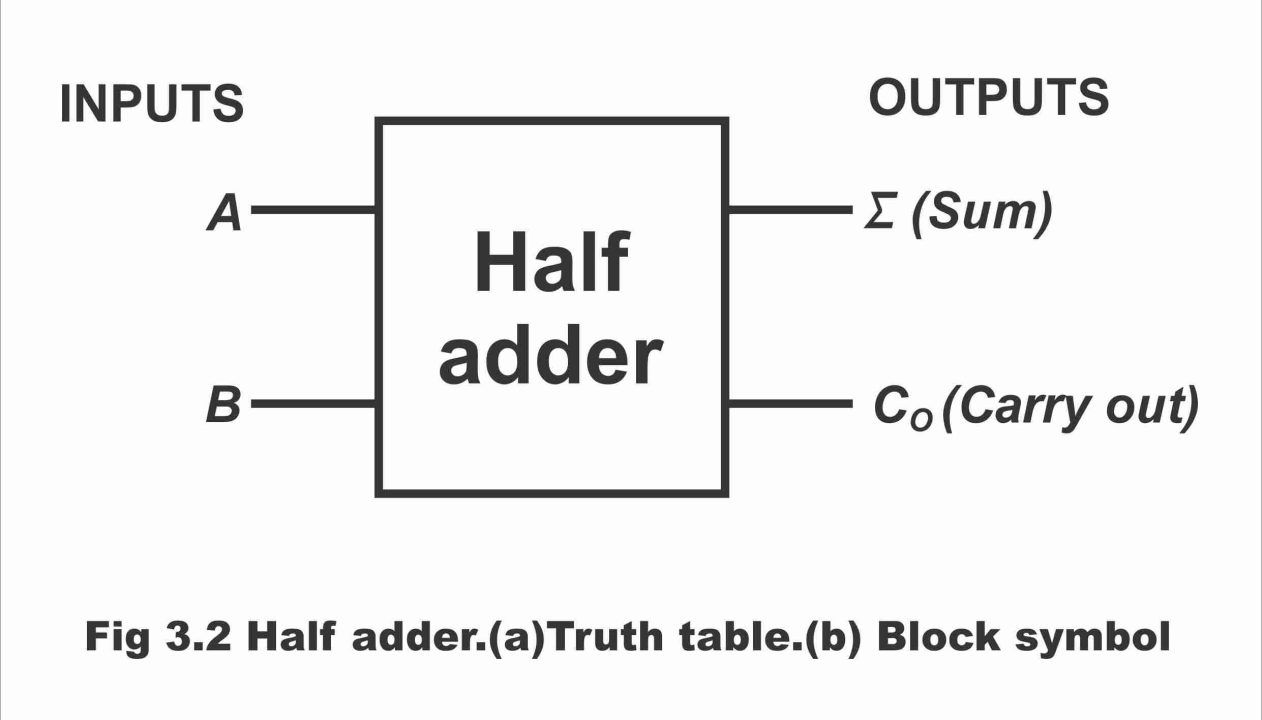
Imagine you're building a simple calculator that can only add two single-digit binary numbers (0 or 1). A half adder is perfect for this task. It takes two inputs, let's call them A and B, and produces two outputs: a SUM and a CARRY. The SUM is the result of adding A and B, while the CARRY represents whether the sum exceeds 1 (and thus needs to be carried over to the next digit, just like in regular addition).

To illustrate, let's run through the possibilities. If A is 0 and B is 0, the SUM is 0 and the CARRY is 0. If A is 1 and B is 0 (or vice-versa), the SUM is 1 and the CARRY is still 0. But here's where it gets interesting: if A is 1 and B is 1, the SUM becomes 0 and the CARRY becomes 1. This represents the binary value of 2 (10 in binary), so the 1 gets carried over.

Essentially, a half adder is like a simplified version of addition. It handles the basics but can't cope with carry-ins from previous additions. It's great for starting an addition process, but not so hot for continuing it. We need something a little more advanced for that.

Think of it like this, a half adder is like trying to assemble a complex piece of furniture with only a screwdriver. You can get started, but you'll quickly realize you need more tools to finish the job. Those "tools" in our digital world are the full adders.

Stepping Up

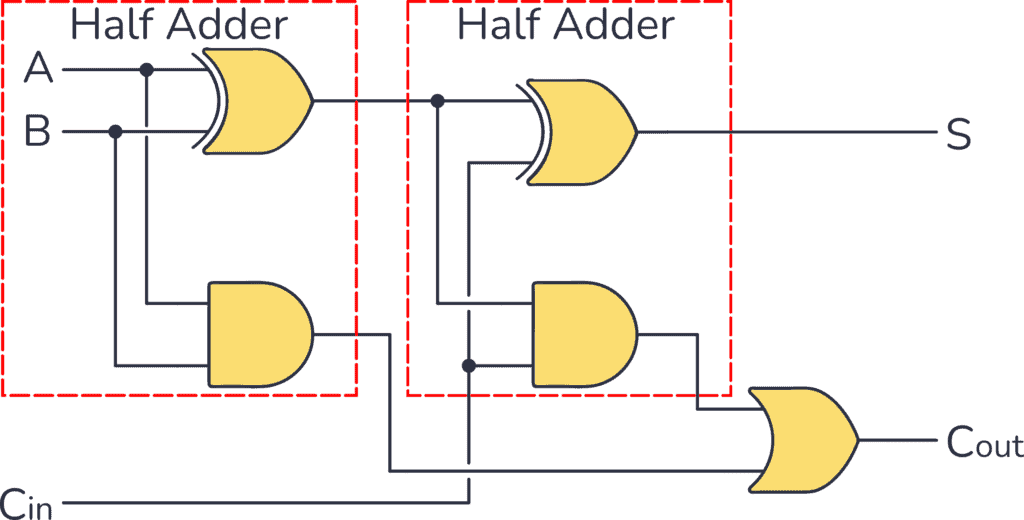
Now, enter the full adder, the big brother of the half adder. Unlike its simpler sibling, a full adder can handle three inputs: A, B, and CARRY-IN. The CARRY-IN is the carry bit from the previous stage of addition. This makes the full adder perfect for adding multi-digit binary numbers, as it can chain together seamlessly.

2. Why the CARRY-IN Matters

Let's say you're adding two binary numbers: 11 and 01. The least significant bits (the rightmost ones) are 1 and 1, which the half adder can handle, producing a SUM of 0 and a CARRY of 1. But when you move to the next digit, you need to add 1, 0, and the carry-in of 1 from the previous stage. That's where the full adder shines.

The full adder also produces two outputs: a SUM and a CARRY-OUT. The SUM is, again, the result of adding the three inputs. The CARRY-OUT is the carry bit that gets passed on to the next stage of addition. This allows us to chain full adders together to handle binary numbers of any length.

A full adder is like having the entire toolbox. You've got your screwdriver (half adder functionality), but you also have wrenches, pliers, and everything else you need to tackle any addition task, no matter how complex.

Think of building a staircase. The half adder helps you build the first step, but the full adders are what allow you to build the rest of the staircase, incorporating the height of the previous steps to make sure everything lines up correctly.

How They Work Together

Half adders and full adders aren't mutually exclusive; they work in tandem to perform binary addition. In a typical multi-bit adder, the first stage (adding the least significant bits) uses a half adder, as there's no carry-in from a previous stage. All subsequent stages utilize full adders to incorporate the carry-out from the preceding stage.

3. A Practical Analogy

Imagine you're running a factory that produces numbers. The half adder is like the initial processing unit, taking in raw materials (the two binary digits) and producing a preliminary product (the sum and carry). The full adders are the subsequent processing units, refining the product by incorporating information from earlier stages (the carry-in) to create the final, polished number.

Without both types of adders, the factory would grind to a halt. The half adder gets the ball rolling, and the full adders keep it moving, ensuring a smooth and efficient production line.

So, next time you're using your calculator or computer, remember the tireless work of these tiny circuits behind the scenes. They're the real MVPs of digital arithmetic!

4. More Than Just Addition

While we've focused on addition, it's important to know that adders are fundamental building blocks for other arithmetic operations as well. Subtraction, multiplication, and division all rely heavily on addition, and therefore on half and full adders. They truly are the foundational circuits of modern computing.

Diving Deeper

Both half adders and full adders are typically implemented using logic gates. These are fundamental electronic circuits that perform basic logical operations such as AND, OR, XOR (exclusive OR), and NOT. Understanding how these gates are interconnected to create adders provides a deeper understanding of their functionality.

5. Under the Hood

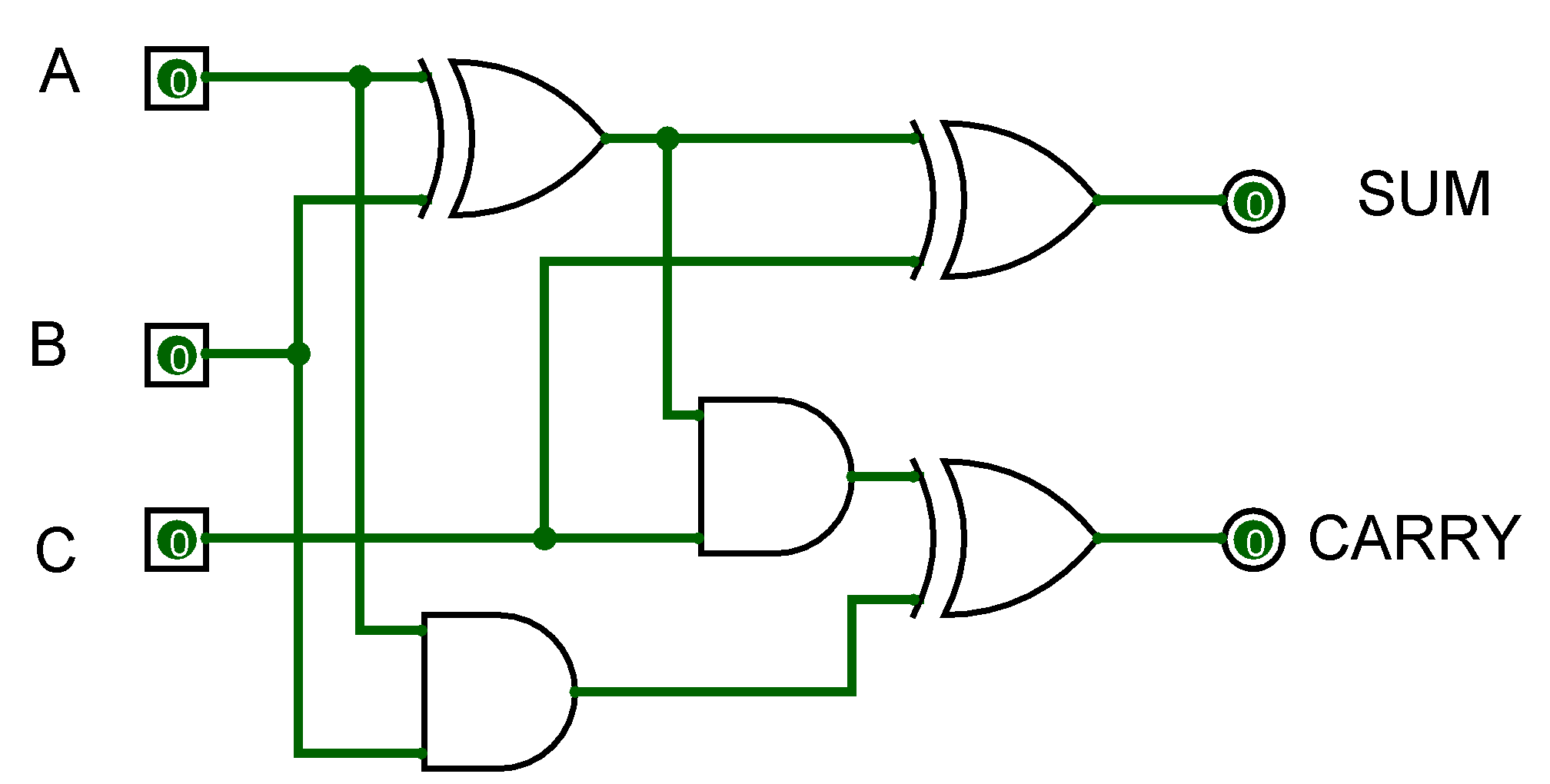
A half adder can be constructed using an XOR gate and an AND gate. The XOR gate produces the SUM output (A XOR B), while the AND gate produces the CARRY output (A AND B). It's a simple yet effective design.

A full adder, on the other hand, requires more logic gates. One common implementation uses two XOR gates, two AND gates, and one OR gate. The first XOR gate combines A and B. The output of this XOR gate and the CARRY-IN are fed into the second XOR gate to produce the SUM output. The two AND gates produce intermediate carry signals, which are then combined using the OR gate to generate the CARRY-OUT.

By understanding the underlying logic gate implementations, you can appreciate the ingenuity and efficiency of these adder circuits.

FAQs About Half Adders and Full Adders

Let's tackle some common questions about these essential digital components.

6. Question 1

Answer: Half adders are great for the first stage of binary addition where there is no carry-in. Full adders are necessary for subsequent stages to incorporate the carry-in from the previous stage, allowing for multi-bit addition.

7. Question 2

Answer: Absolutely! By using a technique called two's complement, you can represent negative numbers in binary. With some clever manipulation (like inverting one of the inputs and adding 1), you can use adders to perform subtraction.

8. Question 3

Answer: Yes, there are variations in the implementation of full adders, often aimed at optimizing for speed or power consumption. For example, carry-lookahead adders are designed to speed up the carry propagation, leading to faster overall addition.